ØxOPOSɆC - Secrets [Crypto]

We all have secrets! And sometimes we need to share them with our online friends, safely... That's easy! - Just implement a very secure, hackerproof™ secret sharing web application!"
URL: https://secret.mbie.me

When you access the website you see the following page:

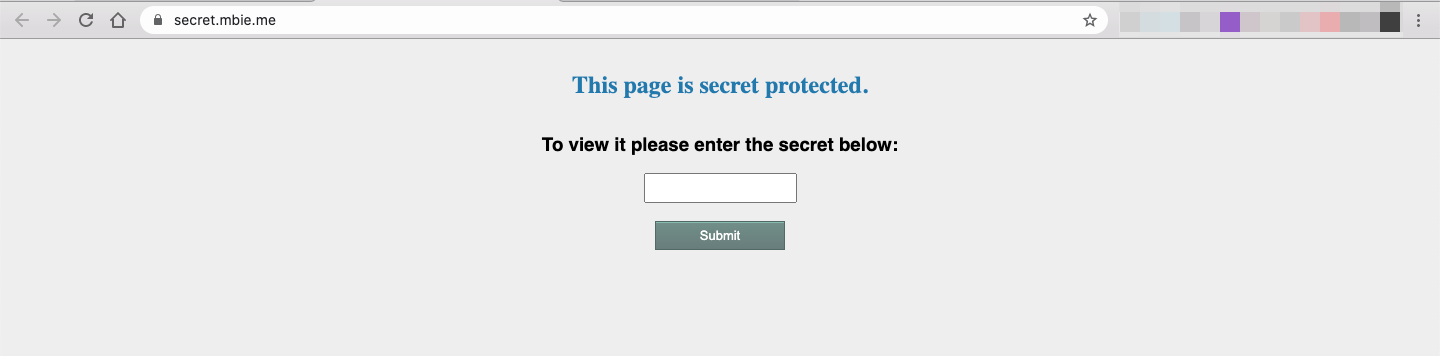
Entering random data on the input field doesn't seem to provide us with any interesting information:

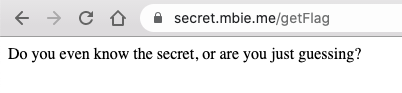
Using wfuzz I found a new page:

~ wfuzz -c --hc 404 -w big.txt https://secret.mbie.me/FUZZ

...
=====================================================================
ID           Response   Lines    Word       Chars       Payload
=====================================================================

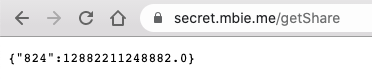
000016081:   200        16 L     42 W       425 Ch      "secret"

The /secret page displays a message with a link to the /getShare page:

The /getShare page retrieves a "secret share", and we can also see from the previous message that collecting 3 of these might be of interest to us, which points in the direction of some cryptographic attack ...

Getting more secret shares

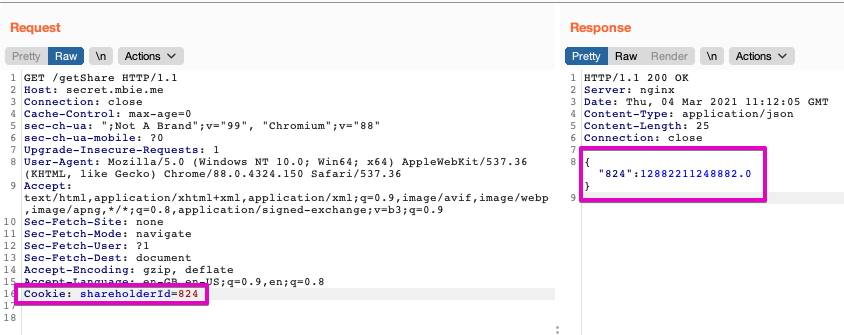
After taking a closer look at the GET request to /getShare we see that we can manipulate the shareholderId value set in the Cookie:

Using Burp Intruder to brute-force this field, we're unable to retrieve the secret share of users with shareholderId's between 1 and 499:

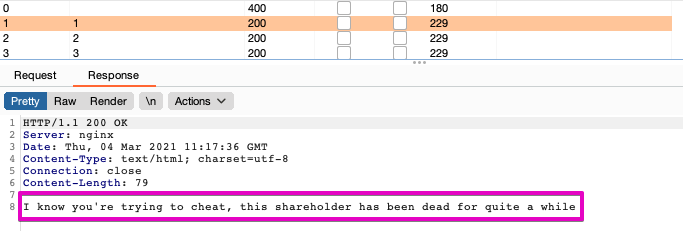
For requests with ID's above 500 we see the following:

{"500":12876858175638.0}
{"501":12876870698406.0}
{"502":12876883245936.0}
{"503":12876895818228.0}
...
{"824":12882211248882.0} [DEFAULT]
{"825":12882231794538.0}
{"826":12882252364956.0}
{"827":12882272960136.0}
...
{"1000":12886208619138.0} 
{"1001":12886233522906.0}
{"1002":12886258451436.0}
{"1003":12886283404728.0}
...
infinite

It wasn't hard to figure out that as we increment the shareholderId the secret share is equal to the previous shareholder's secret share plus a difference that increments by 24672, which means these secrets are not random data encrypted with any typical key, they're something else.

ID    Secret Share        Diff from previous

...
822   12882170231856.0
823   12882190727988.0    +20496132
824   12882211248882.0    +20520894    +24762
825   12882231794538.0    +20545656    +24762
826   12882252364956.0    +20570418    +24762
...

Shamir's Secret Sharing

After a bit of googling I ended up stumbling upon this concept of secret sharing:

(...) a secret is divided into parts, giving each participant its own unique part. To reconstruct the original secret, a minimum number of parts is required. In the threshold scheme this number is less than the total number of parts. Otherwise all participants are needed to reconstruct the original secret.

In this case, we already know that we only need 3 shares to reconstruct the original secret, from the hint on the /secret page.

On the Wikipedia page we can see an example of an implementation of this algorithm in Python, which I adapted to fit the data we've already collected:

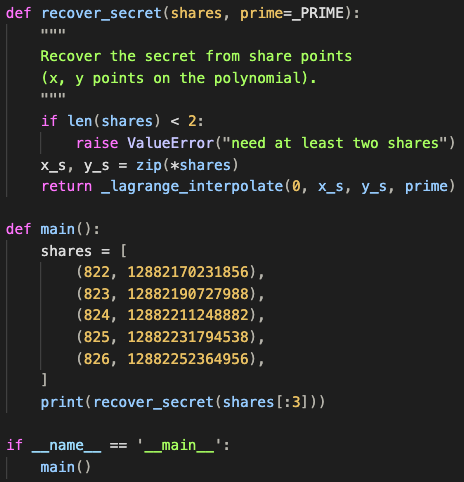
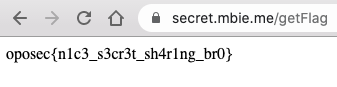
The result is 12873698232138 which when we enter as the secret gives us the flag: